Re-Defining Intelligence: Enhancing Mathematical Reasoning in LLMs

In the evolving field of artificial intelligence, enhancing mathematical and logical reasoning in large language models (LLMs) has become essential to expanding their practical applications. Traditionally, LLMs excel at generating and understanding natural language, but tasks requiring structured reasoning and precise calculations remain challenging.
As these technologies increasingly find their way into specialized domains—like scientific research, financial analysis, and technical problem-solving—there is a pressing need to process text and navigate complex mathematical and logical tasks accurately and consistently. In this blog, we’ll delve into the latest advancements to strengthen these capabilities in LLMs.

Key Concepts in LLMs 

What Are LLMs? 

Fig1: Large Language Models

Large Language Models (LLMs) represent a significant leap in natural language processing capabilities, designed to handle vast amounts of language data and generate coherent, contextually relevant text. These models, including popular examples like OpenAI's GPT-4, Google’s PaLM, and Meta’s LLaMA, are built on transformer architectures—a type of neural network that leverages the self-attention mechanism to process language sequences efficiently. Transformers allow LLMs to capture relationships between words and phrases across extensive contexts, making them highly effective at tasks involving human language.

Mathematical Reasoning vs. Language Processing 

LLMs excel in language processing, which primarily involves understanding patterns in text and generating coherent responses. This type of processing is inherently probabilistic and relies on the model’s ability to predict the next word in a sequence based on prior context. However, mathematical reasoning requires a different approach, as it demands exact calculations, logical deductions, and systematic problem-solving, which go beyond mere pattern recognition. 

Since LLMs were primarily designed as language models, their architecture and training data are not naturally optimized for precise mathematical and logical tasks. Therefore, specialized training and methodologies are necessary to enhance these capabilities.
 

Why Focus on Math and Reasoning? 

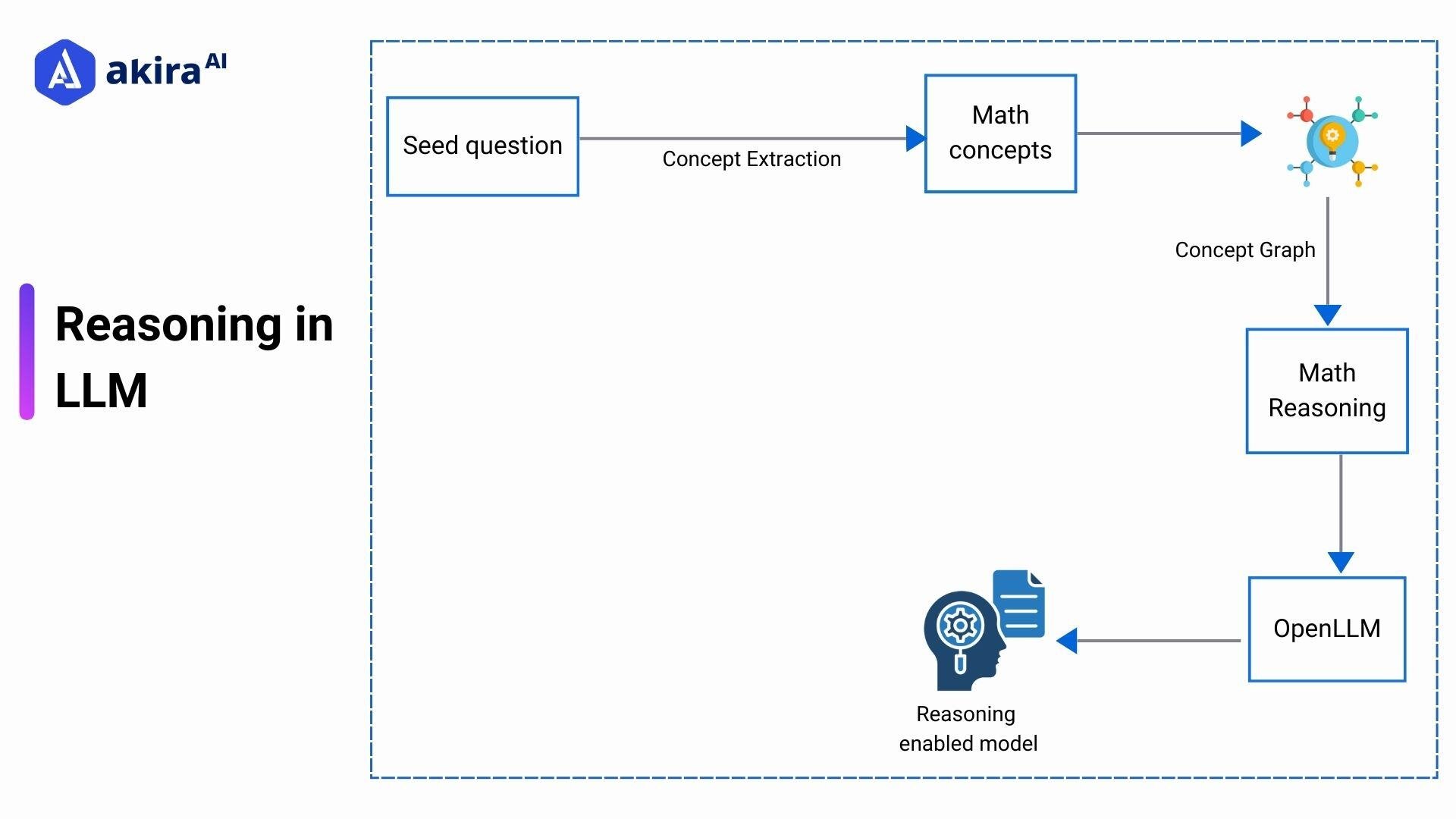Fig2: Reasoning in LLMs

By enhancing LLMs' math and reasoning capabilities, we can expand their utility beyond conversational and creative tasks into areas where rigorous accuracy is essential. Improved reasoning abilities enable LLMs to make more reliable decisions, solve complex equations, and evaluate intricate scenarios. The ability to reason and calculate accurately is not just an added advantage—it’s often a critical requirement for industries that rely on precision and consistency.

Implementation: Enhancing Math and Reasoning in LLMs 

Improving mathematical and reasoning capabilities in Large Language Models (LLMs) involves several advanced techniques and methodologies. These techniques aim to enable LLMs to handle complex calculations, logical inferences, and decision-making processes more accurately.

1. Chain-of-Thought (CoT) Prompting: This approach guides the LLM through a series of logical steps to solve a problem. This method helps the model by structuring its reasoning process, making it more transparent and logical. 

How It Works: 

1. 1. • Initial Prompting: The model is given an initial prompt that outlines the problem. 

      • Sequential Steps: The problem is broken down into smaller steps, and the model is prompted to solve each step in sequence. 

      • Intermediate Verification: The intermediate result is checked for correctness after each step. 

      • Final Aggregation: The final solution is derived by aggregating the intermediate results. 

2. Tree-of-Thought (ToT) Reasoning: This method builds on the CoT approach by exploring multiple reasoning paths in parallel. It is especially useful for problems with multiple potential solutions or paths to the solution. 

How It Works: 

1. 1. • Problem Statement: The model is given a problem statement and generates multiple reasoning paths. 

      • Parallel Exploration: Each path is explored parallel, creating a tree-like structure. 

      • Iterative Refinement: Paths are iteratively refined based on validation feedback. 

      • Convergence: The model converges on the most plausible solution by selecting the best path. 

3. Adding Mathematical and Logical Reasoning Datasets: To develop reliable mathematical and logical reasoning skills in LLMs, it’s essential to use targeted datasets that cover a spectrum of problem types. Datasets like MathQA and GSM8K contain diverse math-related questions, ranging from simple arithmetic to advanced calculus. 

Implementing these datasets for training involves: 

1. 1. • Fine-Tuning the Model: Adding a targeted training phase where the LLM is fine-tuned specifically on these datasets, enabling it to adapt to the language and structure of math and logical problems. 

      • Evaluation and Iteration: Continuously assess model performance on test subsets and iterate over model adjustments to ensure accuracy across different math and logic subfields. 

4. Embedding Structured Knowledge Representations: Structured knowledge representation gives LLMs a "mental map" that can significantly improve logical and reasoning capabilities. Embedding knowledge graphs within an LLM enables it to access predefined logical relationships, which it can use for inference. Knowledge graphs assist in forming inferences by representing knowledge as a network of interconnected facts and concepts.  

Technical Steps: 

1. 1. • Embedding Knowledge Graphs: Embedding representations from knowledge graphs can be done by creating structured embeddings, where entities and relations are transformed into dense vectors. These vectors serve as part of the model’s input layer, allowing the LLM to utilize graph-based relationships in its reasoning processes. 

5. In-Context Learning and Few-Shot Reasoning: In-context learning is a technique that allows LLMs to improve their problem-solving skills by using example problems within a prompt. Rather than extensive re-training, this method presents the model with few-shot examples to guide it in solving similar tasks. 

• How In-Context Learning Works: During the prompting phase, the LLM provides examples of how similar problems have been solved. These examples serve as a reference, and the model learns to extrapolate solutions based on these patterns. 

• Few-Shot Reasoning: Using few-shot reasoning, an LLM can handle various new tasks by observing several demonstrations. This is particularly effective in enhancing the model’s accuracy without requiring substantial fine-tuning.

Technical Steps: 

1. 1. • Prompt Design: Carefully design prompts with few-shot examples that cover a range of mathematical or logical tasks tailored to the desired level of complexity. 

      • Testing  Test prompts across different types of math problems or logical inferences ensures the model can generalize beyond the examples provided. 

      • Iterative Improvement: Use evaluation results to refine the prompt structure, adding layers of complexity in examples to enhance reasoning accuracy further. 

Example: 

1. The odd numbers in this group add up to an even number: 4, 8, 9, 15, 12, 2, 1. 

A: The answer is False. 

2. The odd numbers in this group add up to an even number: 17,  10, 19, 4, 8, 12, 24. 

A: The answer is True. 

3. The odd numbers in this group add up to an even number: 16,  11, 14, 4, 8, 13, 24. 

A: The answer is True. 

Key Benefits of Enhanced LLMs

Advanced reasoning techniques within LLMs offer many benefits for improving mathematical ability and performance. 

1. Improved Accuracy: Advanced reasoning methods generate solutions with enhanced accuracy, breaking problems into manageable steps and checking intermediate results. 

2. Robust Problem-Solving: Structured approaches like CoT and ToT enhance robustness in problem-solving by exploring multiple paths and getting better results on iterations. 

3. Scalability: Multi-agent systems allow scalable improvements using the power of multiple models, which can work on parts of a problem simultaneously. 

4. Reduced Hallucinations: Collaborative verification reduces the instances of erroneous outputs, known as hallucinations, by ensuring that multiple agents validate each step. 

5. Versatility: These methods can be applied to different LLMs and problem domains, making them versatile tools for varied applications. 

Use Cases of Mathematical Reasoning in LLMs

Adding advanced reasoning capabilities to LLMs opens up use cases across many sectors, promoting increased productivity and better decisions. 

1. Maintenance: In the maintenance area, better reasoning capabilities in LLMs can be useful for streamlining predictive maintenance, troubleshooting, and resource optimization. With advanced reasoning capabilities, organizations can predict equipment failures using historical performance data and maintenance logs by utilizing LLMs. 

2. HR Operations:  The improved reasoning in LLMs can help automate complex decisions in hiring, employee management, and the training process in HR operations. Advanced reasoning LLMs can judge candidates' qualifications by analyzing application data, calculating their skills fit, and suggesting possible role fits. 

3. Customer Support: LLMs' improved reasoning capabilities enable them to present quicker and more accurate answers in customer support. Hence, they are good at answering complex questions and enhancing customer satisfaction. 

4. IT Operations: Reasoning-enhanced LLMs in IT operations can monitor, manage, and resolve IT issues much faster. This reduces downtime and increases operations resilience. Pattern reasoning over error logs and performance metrics helps LLMs solve common problems. 

5. Security Operations: LLMs have advanced reasoning capabilities, which would improve security operations by enhancing threat detection, response strategy, and risk assessment. The ability to analyze multiple sources of real-time data enables LLMs to identify patterns associated with security threats. 

Prompt Hub on Akira AI 

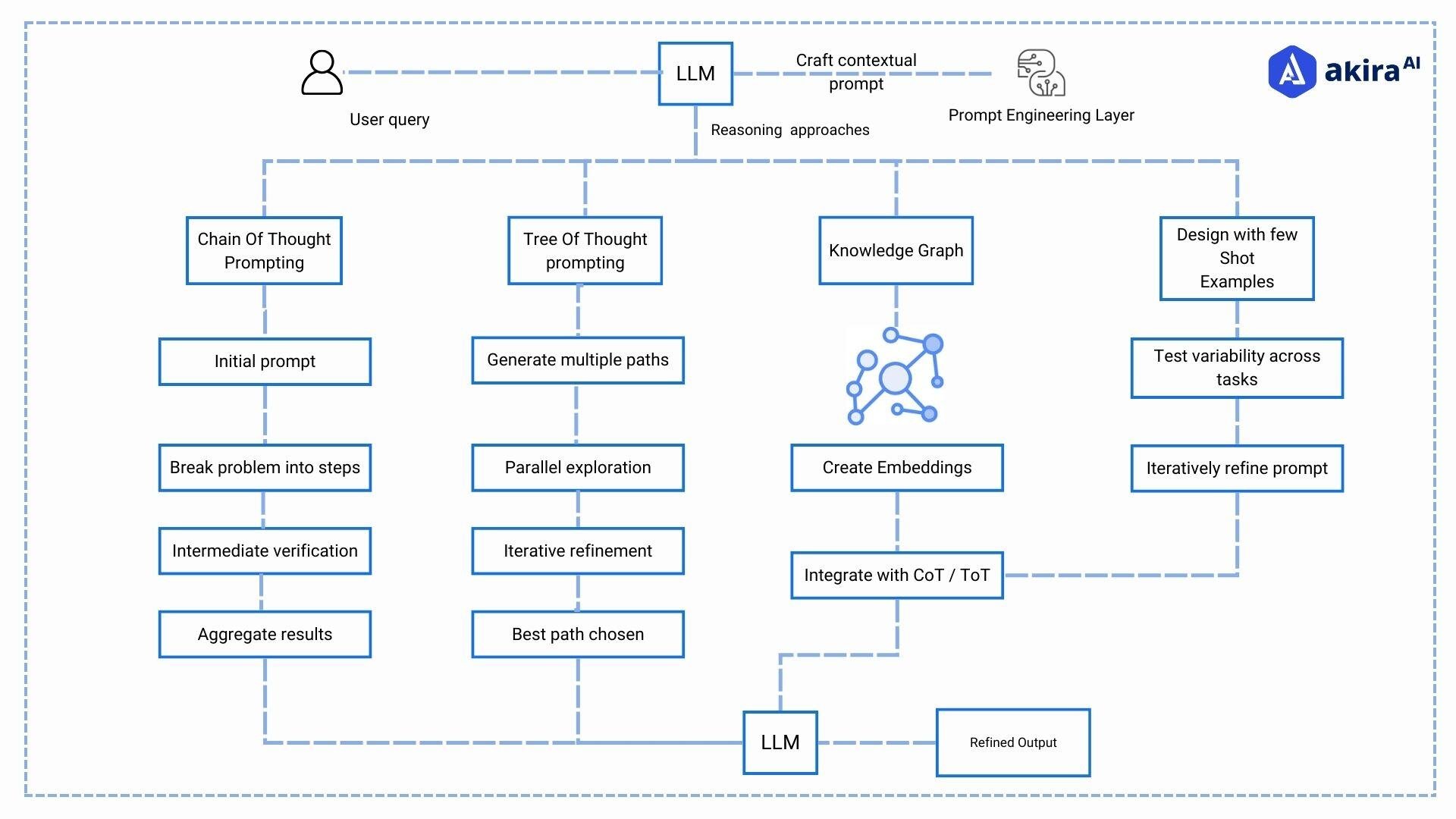Fig3: Architecture Diagram of Prompting Strategies for Reasoning

Akira AI is an advanced agentic AI platform, through which users can create and deploy intelligent agents and finetune LLM that can be custom-tailored to specific business needs. 

1. Prompt Library on AkiraAI serves as a foundational tool, offering predefined prompts tailored for specific types of reasoning and calculation tasks. These prompts guide the model through multi-step problem-solving processes, mimicking human-like logical deduction. The flexibility of our prompt library also allows users to customize prompts or create few-shot reasoning examples for in-context learning. 

2. Integration with structured datasets such as MathQA and GSM8K is straightforward on AkiraAI. Users can upload or select datasets that target specific math and reasoning skills, enabling focused fine-tuning of models. AkiraAI also supports knowledge graphs and embeddings, allowing LLMs to tap into structured, logical pathways and relationships when reasoning.

Challenges in Improving Capabilities in LLMs 

While advanced LLM capabilities offer several advantages, challenges remain that need to be overcome for effective deployment. 

1. Computational Resources: LLM has a large computational cost for training and implementations. Hence, they are a major concern as they require much computing power and memory. 

2. Scalability problems: Scaling multiple agents is rather problematic for large-scale applications. Coordinating several agents and their respective interactions becomes complex. 

3. Model Interpretability: These methods create complex reasoning paths that are difficult to understand. Sometimes, it becomes difficult to understand why the model arrived at that solution. 

4. Data Quality: High-quality, diverse datasets are needed to train and validate models. Poor-quality data can lead to inaccurate results. 

5. Dynamic Search: There are limitations in the dynamic exploration of the reasoning search space. Ensuring the model explores all relevant possibilities without missing critical paths can be difficult. 

Future Directions: Advancements in Math and Logic for LLMs 

Several promising directions will bring the math and logic capability of LLMs ahead. 

1. Greater utilization of autonomous multi-agent systems: Because AI is continuously evolving, multi-agent systems will work autonomously and be coordinated across applications. 

2. Integration with Computation Tools: Integrating LLM with advanced computational tools can significantly enhance its functionalities. For example, a model can execute real-time calculations, simulations, and visualizations beyond text alone. 

3. Advanced Symbolic Reasoning: The symbolic reasoning skills will enable the LLMs to manipulate and understand mathematical expressions and equations. Such skills are integral to performing abstract math concepts and serve as a means to deeper logical reasoning. 

4. Dynamic Prompt Systems. The dynamic prompt systems are meant to guide the users to form questions; better interactions will follow. Tailored prompts will help users better articulate complex math problems, thus being more accurate and relevant to responses from the models. 

5. Interdisciplinary Approaches: Exploring interdisciplinary approaches by incorporating principles from cognitive science and education can enhance LLMs’ reasoning abilities.

Conclusion: Mathematical Reasoning in LLMs

The advancement of mathematical and reasoning capabilities in large language models marks a significant milestone in the AI agent landscape. While current innovations like CoT and ToT show promising results, they also underscore the complexity of embedding human-like problem-solving abilities in AI systems. As this field continues to evolve, the focus must remain on developing robust, reliable, and verifiable mathematical reasoning frameworks. These developments push the boundaries of LLMs and bring us closer to creating more capable and trustworthy responses that can effectively support human decision-making across various domains.